1 미터 길이의 막대기를 무작위로 세 조각으로 잘랐을 때, 잘린 세 개의 막대기로 삼각형을 만들 수 있을 확률은?

해답을 알고나면 퍼즐은 더이상 의미/재미가 없으므로, 아래 해답을 보기 전에 반드시 혼자서 풀어 볼 것!

혹시 아래 해법에 동의하지 않거나, 다른 (더 재미있는) 해법이 있다면 댓글 혹은 메일 주세요!^^

해법 1

우선, 1미터 길이의 막대기를 세 개의 작은 막대기로 자르는 경우의 수를 생각해보자. 한 막대기의 길이(\(x\))를 알고 나면, 두번째 막대기의 길이(\(y\))는 원래 1 미터의 길이에서 첫 막대기의 길이를 뺀 값까지, 즉 \(0\)에서 \(1 - x\) 사이의 값을 가지게 되고, 나머지 세번째 막대기는 자동으로 1 미터에서 첫 두 막대기의 길이를 뺀 \(1 - x - y\)의 길이를 갖게 된다. 다시 말해, 가능한 모든 경우의 수는 두 개의 막대기의 길이\((x, y)\)로 완벽하게 표현을 할 수 있고, 이 가능한 범위를 그래프로 그리면 아래와 같다.

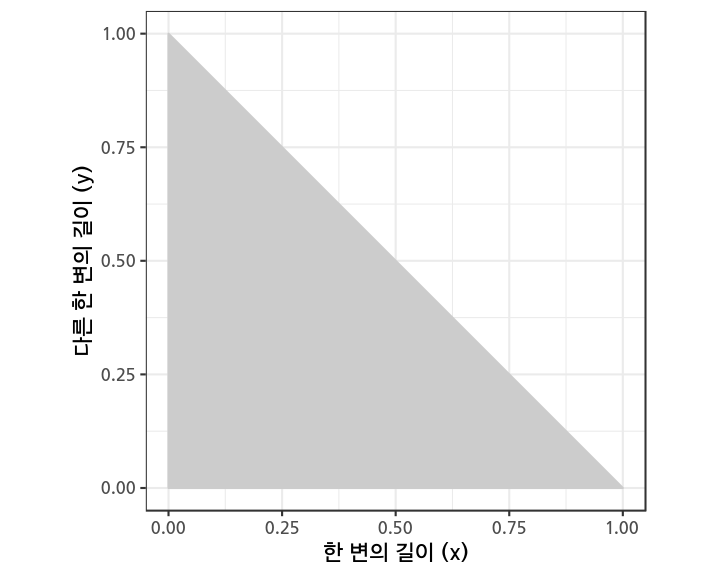
1 미터 길이의 막대기에서 무작위로 자른 세 개의 막대기의 길이를 \(x, y,\) 그리고 \(1 - x - y\)로 쓸 수 있다.

중학교 수학에 의하면, 길이가 \(x, y, 1 - x - y\)인 세 개의 막대기로 삼각형을 만들기 위해서는 두 개의 길이의 합이 나머지 한 개 길이의 합 보다 커야한다. 즉,

$$ \begin{align} x + y & > 1 - x - y \\\
(1 - y - x) + x & > y \\\
(1 - y - x) + y & > x \end{align} $$ 를 만족해야 하고, 이를 정리하면 다음과 같다: $$ \begin{align} y & > \frac{1}{2} - x \\\
y & < \frac{1}{2} \\\
x & < \frac{1}{2}. \end{align} $$

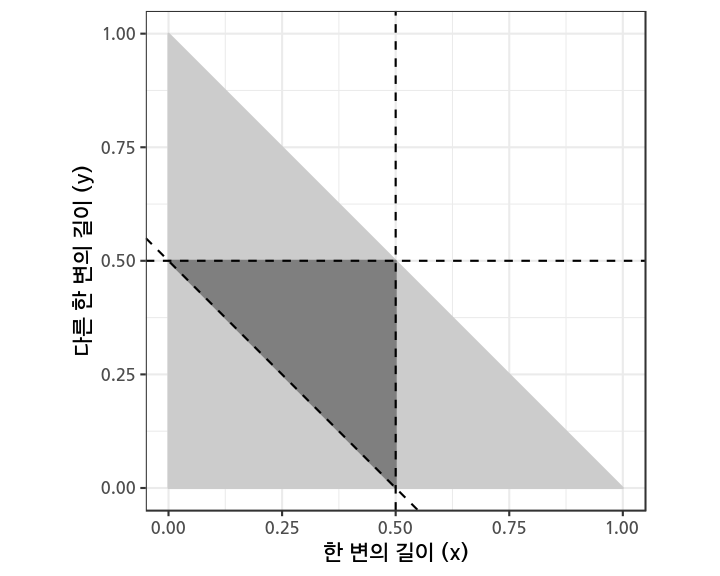
어떤 특정 경우(이벤트)의 확률을

모든 가능한 경우의 수 중 해당 경우(이벤트)가 발생하는 비중

으로 정의한다면, 삼각형을 만들 수 있는 확률은, 아래 그림에서 가능한 모든 막대기 길이의 경우를 나타낸 큰 삼각형 중, 삼각형을 만들 수 있는(위 조건을 만족하는) 경우의 수를 나타낸 작은 삼각형이 차지하는 비중, 즉 1/4이다.