어느날, 한 신사가 희안하게 생긴 동전을 꺼내 든다. 동전을 던져서 앞면이 나올지 뒷면이 나올지 내기를 하자고 한다. 먼저 동전을 10번 던질테니, 그 결과를 보고, 11번째 동전을 던졌을 때 앞면이 나올지, 뒷면이 나올지에 돈을 걸자고 한다.

10번을 던진 결과는 다음과 같았다:

앞 뒤 앞 앞 앞 뒤 앞 앞 앞 앞 

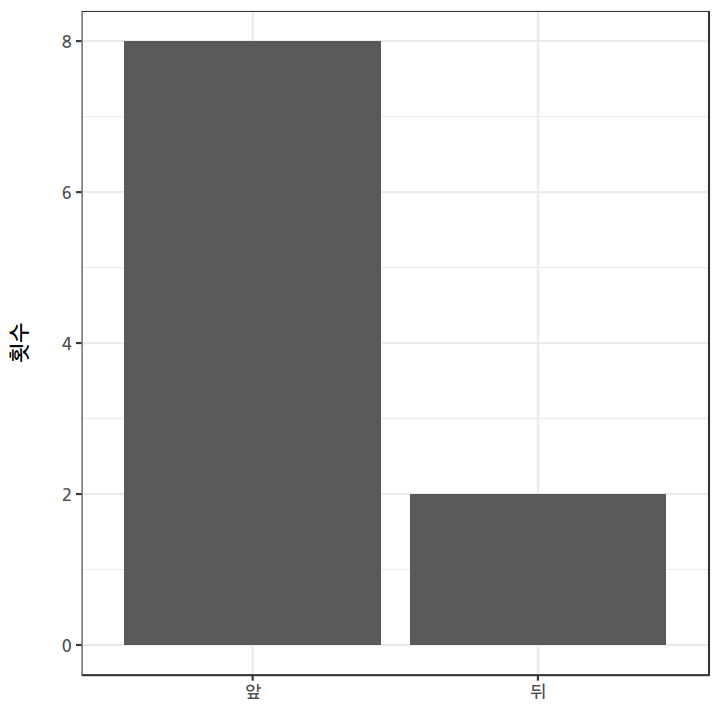
위 결과를 본 신사는, 다음번에 뒷면이 나오면 만원을 줄테니, 만약 앞면이 나오면 9천원을 달라고 한다¹.

내기를 받아들이겠는가?

교과서적 해답

중/고등학교 수학 시간 첫 확률 수업을 기억한다면, 대답은 간단하다:

1. 동전에는 앞면과 뒷면, 두 가지의 경우의 수가 있다
2. 앞면이나 뒷면이 나올 확률이 같다고 가정한다면, 앞면이 나올 확률이나 뒷면이 나올 확률은 반반(\(\frac{1}{2}\))이다
3. 동전을 몇 번을 던지든, 앞(뒷)면이 나올 확률은 변하지 않기 때문에, 과거에 던진 결과가 앞으로 던질 결과에 영향을 미치지 않는다
4. 결과적으로, 50%의 확률로 만원을 얻거나 9천원을 잃을 수도 있으니, 이 내기의 기대값(평균 가치)은 500원(이득)이다 (다시 말해, \(\frac{10 - 9}{2}=0.5\))

위 논리에 동의한다면, 내기를 받아들이는 것이 500원어치 이득일 것이다.

상식

교과서적 “정답"에도 불구하고, 막상 실제로 위와 같은 내기를 받아들이기에는 조금 불편한 점이 있다.

기대값을 기대할 수는 없다

우선 문제가 되는 부분은, “기대값"이란 말로 표현한 위 내기의 “가치"가 “500원'‘이라는 점이다.

내기를 받아들인다면, 동전을 11번째로 던진 후, 발생 가능한 결과는 딱 두 가지 뿐이다:

• 앞면이 나와서 신사에게 9천원을 준다 (-9천원)
• 뒷면이 나와서 신사로부터 만원을 받는다 (+만원)

어디에도 500원의 이득을 보는 상황은 발생하지 않는다. 내기의 “기대값"이 500원이라는 말은 —앞의 다양한 가정에 동의한다면—

• 위 내기를 받아들이는 것과,
• 내기 없이 당장에 500원을 받고 집에 가는 것

두 상황에 대해 특별히 선호하는 것이 없다는 이야기일 뿐이다.

다시 말해, 신사가 “내기를 할래, 400원 받고 집에 갈래?” 하고 묻는다면, 내기를 하고, 반대로 “내기를 할래, 600원 받고 집에 갈래?” 하고 묻는다면, 600원을 받고 집에 가겠다는 이야기다.

만약, 방금 전 문단의 예시에 동의하지 않는다면, 이는 교과서적 해답의 가정에 동의하지 않는다는 이야기고, 상식적인 사람이라면 충분히 그럴 수 있다.

뒷면이 나올 진짜 확률은?

교과서적 해답은 크게 두 가지 가정을 전제하고 있다:

• 앞면이 나올 확률과 뒷면이 나올 확률은 같다
• 동전을 아무리 던져도, 앞(뒷)면이 나올 확률은 변하지 않는다

하나씩 자세히 살펴보자.

뒷면이 나올 확률과 앞면이 나올 확률은 같다?

확률에 관한 수업을 많이 듣고, 연습문제 등을 많이 풀어 본 사람일 수록, 별 생각 없이 이 가정을 받아들이기 쉽다. 확률을 처음 배울 때는 (편의상)

“앞/뒤가 나올 확률이 각각 50%인 동전이 있다 …”

“6면이 모두 같은 확률을 가진 주사위 …”

“항아리 속에 검정 구슬과 빨강 구슬 …”

“무작위로 섞인 카드 52장 …”

등으로 시작하고, 늘 “모든 경우의 수가 같은 확률을 가진다"고 가정한다.

이런 “연습문제"에 익숙해지다보면, 어느새 “동전을 던져서 앞면이 나올 확률은 뒷면이 나올 확률과 똑같이 50%이다"가 하나의 진리처럼 받아들여진다.

하지만, 현실적으로 —그리고 상식적으로— 조금만 곰곰히 생각을 해보면, 오히려 앞면과 뒷면이 나올 확률이 정확히 똑같은 동전을 생산하기는 거의 불가능하다. 더 나아가서, 동전을 던졌을 때 바람의 방향, 동전의 모양에 따른 저항 등 수없이 많은 요소를 고려한다면, 동전이 어느 면으로 떨어질지 보다 정확하게 예측 할 수도 있을 것이다.

앞(뒷)면이 나올 확률은 변하지 않는다?

앞면과 뒷면이 나올 확률이 굳이 같지 않을 수 있다고 하자. 그러면, 시간이 지남에 따라, 혹은 동전을 던질 때마다, 같은 동전의 앞(뒷)면이 나올 확률은 변화 할 수 있을까?

얼핏 생각하기엔 당연히 변하지 않아야 할 것 같다. 대부분의 확률 수업에서는, “확률"이라는 것을 어느 물건(동전, 카드, 주사위)의 본질적인 속성으로 소개를 하고 있고, 이를 당연하게 받아들이는 경향이 있기 때문이다.²

하지만, 이 또한 잠시 생각을 해보자. 두 가지 상황을 상상해 볼 수 있다:

1. 누군가가, (지구) 어디에선가, 우리는 알지도 못하고 보지도 못한 어느 동전을 던진다고 한다. 분명한 것은 딱 하나 – 이 동전에 두 개의 면이 있다는 것이다
2. 오랜 시간(수백년?)에 걸쳐 위 미지의 사람이 이 동전을 끊임 없이 —수 천, 수 백만 번, 그 이상— 던졌는데, 뒷면은 딱 한 번 나오고, 계속 앞면이 나왔다

1번 상황만을 가지고 봤을 때, 이 동전의 “앞면이 나올 확률"은 뭐라고 해야할까? 아무것도 모르는 상황에서, 나라면, 50:50, 반반이라고 할 것이다. 가능한 경우의 수가 두 가지라는 것 말고는 아는게 없다면, 어느 한 면이 다른 한 면보다 더 큰 확률을 가진다고 믿을 이유가 없기 때문이다. (한 편으로는, 어느면이 앞/뒤인지도 딱히 말 할수 없다!)

그런데 2번 상황이라면, 1번 상황에서 말한 것과 물리적으로는 똑같은 동전이라 하더라도, 나는 앞으로 이 동전을 던졌을 때 앞면이 나올 확률은 아주아주 높다고 할 것이다.

즉, —“앞/뒷면이 나올 확률이 같다"처럼 비현실적인 가정을 전제하지 않고서는— 확률이라는 것은 단지 내가 알고 있는 정보, 그리고 불확실한 결과(앞면이냐 뒷면이냐)에 대한 내 믿음의 표현이라고 생각 할 수 있고³, 그렇게 생각한다면, 과거에 관찰한 결과들이 앞으로의 결과에 대한 나의 믿음(확률)에 영향을 주지 말라는 법도 없지 않을까?

결론

그럼, 결론적으로, 내기는 해야되냐 말아야 되냐?

지금까지의 이야기에 모두(혹은 부분적으로?) 동의한다면, 이는 “11번째 던졌을 때, 동전이 앞면으로 떨어질 확률"에 대한 각 개인의 믿음에 달려 있다.

아래 그래프를 보면, 이 확률에 대한 믿음에 따라, 내기의 기대값이 어떻게 달라지는지 볼 수 있는데, 만약 52.63% 이하라고 생각한다면 내기를 해볼만 하고(기대값이 0보다 크다), 그렇지 않다면 그냥 뒤돌아서서 가던 길을 가는 편이 낫다고 할 수 있다.

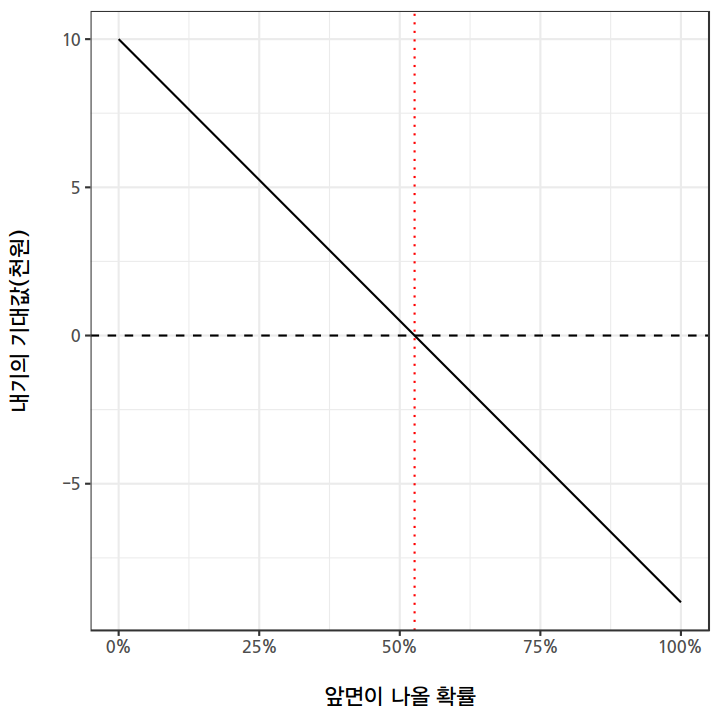
처음 10번 던진 것 중 앞면이 8번 나왔음을 감안했을 때, 당신이라면 내기를 하겠는가, 안하겠는가?⁴

---

1. 판돈이 크면 더 재밌겠지만, 너무 커지면 각 개인의 위험 선호도(risk preference)를 감안하지 않을 수가 없어서, 일단은 푼돈을 예로 들자. ↩︎

2. 굳이 확률 덕후질을 하자면, 여기서 “확률이란 무엇인가?“하는 보다 본질적인 질문을 할 수도 있다. 동전에게 “앞면으로 떨어질 확률"이란 속성이 과연 있는건지, 아니면 “동전이 앞면으로 떨어질 확률"이라는 추상적 개념에 대해, 각 개개인이 가지고 있는 정보에 따라 주관적으로 변화하는 확률에 대한 믿음만이 존재하는지 따져 볼 수 있다. 이중 후자가 “베이지안” 확률의 근간이고, 나는 개인적으로 그 이론을 따른다. 하지만, 여기서 이런 얘기를 풀어 가기엔 너무 덕후 같아 보이니까, 일단 여기까지만 하자. ↩︎

3. 물론, 이것도 하나의 입장일뿐, 이에 대해 극심하게 반발하는 사람들도 있다… ↩︎

4. 이 문제에 대해서도 여러가지 입장/접근방법이 있지만, 그건 또 다른 내용의 글이 되기 때문에, 오늘은 여기까지! ↩︎